13. vaje iz Matematične fizike - nadomeščanje 30. 12. 2025

Difuzijska enačba brez izvorov z difuzijsko konstanto \( D = 1 \) je oblike

\[ \nabla ^2 T = \frac{\partial T}{\partial t}. \]

Problema se bomo v tem primeru lotili s prestavitvijo problema v Fourierov prostor.

Funkcijo \( f \) v prostoru \( \mathbb{R}^n \) pretvorimo v Fourierov prostor preko

\[ \hat{f} \left( \vec{k}, \omega \right) = \frac{1}{\sqrt{2 \pi}^{n + 1}} \int\limits_{}^{} f \left( \vec{x}, t \right) \exp \left\{ - \mathrm{i} (\vec{k} \cdot \vec{x} - \omega t ) \right\} \, \mathrm{d} ^n x \, \mathrm{d}t. \]

Koristni sta identiteti

\[ \widehat{\frac{\partial f}{\partial x_{j}} } \left( \vec{k}, \omega \right) = \mathrm{i} k_j \hat{f} \left( \vec{k}, \omega \right) \quad \text{ in } \quad \widehat{\frac{\partial f}{\partial t}} \left( \vec{k}, \omega \right) = - \mathrm{i} \omega \hat{f} \left( \vec{k}, \omega \right) \]

Rešujemo enačbo v eni dimenziji

\[ \left( \frac{\partial }{\partial t} - \frac{\partial ^2 }{\partial x ^2} \right) G \left( x - x_0, t - t_0 \right) = \delta (x - x_0 ) \delta(t - t_0). \]

Greenovo funkcijo lahko označimo tudi z \( G \left( x, x_0, t ,t_0 \right) \). Za \( x_0 = 0 \) in \( t_0 \) rešujemo enačbo

\[ \left( \frac{\partial }{\partial t} - \frac{\partial ^2 }{\partial x ^2} \right)G (x, t) = \delta(x) \delta(t). \]

Reševanje sedaj prestavimo v Fourierov prostor preko Fourierove transformacije in sedaj imamo enačbo

\[ \left( - \mathrm{i} \omega + k ^2 \right) G (k , \omega) = \frac{1}{2 \pi}. \]

Greenova funkcija v \( k, \omega \) prostoru je tako

\[ G (k, \omega) = \frac{\mathrm{i}}{2 \pi} \frac{1}{\omega + \mathrm{i} k ^2}. \]

Zanima pa nas Greenova funkcija v prostor \( x, t \), kar pomeni, da moramo narediti inverzno Fourierovo transformacijo

\[ G (x, t) = \frac{\mathrm{i}}{\left( 2 \pi \right) ^2} \int\limits_{\mathbb{R} ^2}^{} \frac{1}{\omega + \mathrm{i} k ^2} \exp \left\{ \mathrm{i }k x - \mathrm{i} \omega t \right\} \, \mathrm{d} k \, \mathrm{d} \omega . \]

Ta integral bomo rešili s pomočjo Cauchyjevega izreka in izreka o residuih, ki ima obliko

\[ 2 \pi \mathrm{i }I_{\gamma} (w) f(w) = \oint\limits_{\gamma}^{} \frac{f(z)}{z - w} \, \mathrm{d} z, \]

kjer je \( \gamma \) zaključena zanka in \( I_{\gamma} \) označuje ovojno število in je odvisno od orientacije.

Integral bomo najprej izračunali za \( \omega \). Želimo izvrednotiti integral

\[ \int\limits_{-\infty}^{\infty} \frac{1}{\omega + \mathrm{i} k ^2} \exp \left\{ - \mathrm{i} \omega t \right\} \, \mathrm{d} \omega. \]

Zamislimo si kompleksno ravnino. Naš integral poteka po realni osi, ki je abscisa. Imamo dve možnosti za zaključitev zanke v neskončnosti. Za čas \( t < 0 \) bomo vzeli polkrožnico, katere radij \( R \) gre proti \( \infty \) in se nahaja na pozitivni imaginarni ravnini, saj gre v tem primeru eksponent v integralu proti \( 0 \) z večanjem radija \( R \). Z zaključeno zanko ne zajamemo nobenega pola, kar pomeni, da je vrednost integrala po zaključeni zanki \( 0 \).

Za čas \( t > 0 \) pa si izberemo pokrožnico z enakim radijem \( R \to \infty \) (na sliki označeno z rdečo potjo), ki pa se nahaja v negativni imaginarni polravnini. S tem tudi zaobjamemo pol, ki se nahaja pri \( \omega = - \mathrm{i}k ^2 \), vendar je ovojno število \( I_{\gamma} = -1 \), saj je negativno orientirana zanka. Za negativen čas bi integral po tej polkrožnici divergiral.

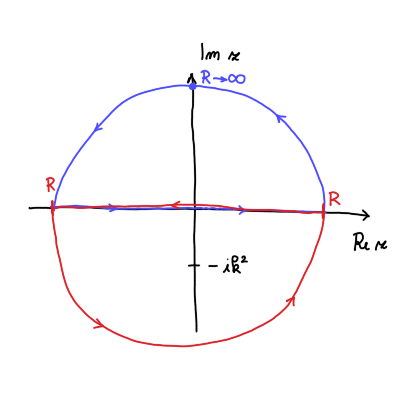
Torej

\[ \int\limits_{- \infty}^{\infty} \frac{1}{\omega + \mathrm{i}k ^2} \exp \left\{ - \mathrm{i} \omega t \right\} \, \mathrm{d} \omega = \begin{cases} 0 &; t < 0 \\ -2 \pi \mathrm{i} \exp \left\{ - k ^2 t \right\} &; t > 0 \end{cases} = H (t) 2 \pi \mathrm{i} \exp \left\{ - k ^2 t \right\} \]

Rešitev v koordinati \( k \) pa je

\begin{align*} G (x, t) &= \frac{1}{2 \pi} H(t) \int\limits_{\mathbb{R}}^{} \exp \left\{ - k ^2 t + \mathrm{i} k x \right\} \, \mathrm{d} k \\ &= \frac{1}{\sqrt{4 \pi t}} \exp \left\{ - \frac{x ^2}{4 t} \right\} H(t). \end{align*}

Greenova funkcija v \( n \)-dimenzijah in na neskončnem območju je tako

\[ G_{\infty} \left( \vec{r}, \vec{r}_0, t, t_0 \right) = \left[ 4 \pi D (t - t_0) \right] ^{-\frac{n}{2}} \exp \left\{ - \frac{\left| \vec{r} - \vec{r}_0 \right| ^2}{ 4 D (t - t_0)} \right\} H(t - t_0). \]

Posplošena Greenova formula za enačbo

\[ \left( \frac{\partial }{\partial t} - D \nabla ^2 \right) T \left( \vec{r}, t \right) = f \left( \vec{r}, t \right) \]

je

\begin{align*} T \left( \vec{r}, t \right) = &\int\limits_0^t \int\limits_{\mathcal{D}}^{} G \left( \vec{r}, \vec{r}_0, t, t_0 \right) f \left( \vec{r}_0, t \right) \, \mathrm{d} ^n \vec{r}_0 \, \mathrm{d} t \\ &+ \int\limits_{\mathcal{D}}^{} T \left( \vec{r}_0, 0 \right) G \left( \vec{r}, \vec{r}_0, 0, 0 \right) \, \mathrm{d} ^n \vec{r}_0 \\ &+ D \int\limits_0^t \int\limits_{\partial \mathcal{D}}^{} \left[ \frac{\partial }{\partial \vec{n}_{0}} T \left( \vec{r}_0, t_0 \right) G \left( \vec{r}, \vec{r}_0, t, t_0 \right) - T \left( \vec{r}_0, t_0 \right) \frac{\partial }{\partial \vec{n}_{0}} G \left( \vec{r}, \vec{r}_0, t, t_0 \right) \right] \, \mathrm{d} ^{n - 1} S_0 \, \mathrm{d} t_0 \end{align*}

Prvi člen predstavlja partikularno rešitev, drugi člen predstavlja začetni pogoj ter tretji člen je rešitev homogene enačbe.

Uporabili bomo Greenovo funkcijo na neskončnem območju, ki jo pretvorimo na končno območje preko zrcaljenja.

Poljubno točko \( x_0 \in [0, a] \) prezrcalimo preko točke \( x_0 \), ki poskrbi za \( 0 \) Greenove funkcije v meji \( x = 0 \). To bo točka \( x_1^- = - x_0 \). Potrebujemo tudi, da je Greenova funkcija na meji \( x = a \) ničelna. To bo točka \( x_1^+ = 2a - x_0 \). Hkrati pa potrebujemo tudi točko, ki bo točko \( x_1^- \) na meji prezrcalila v \( 0 \). To bo točka \( x_2^+ = 2a + x_0 \). Novi pridobljeni točki se morata ponovno slikati v meji na nič, kar dosežemo s točka \( x_+ = - 2a + x_0 \) in \( x_- = -2a - x_0 \). Prva slika točko \( x = 2a + x_0 \), druga slika točko \( x = 2a - x_0 \).

Opazimo, da imamo zaporedje

\begin{align*} x_{0, n}^+ &= x_0 + 2 na \\ x_{0, n}^0 &= -x_0 + 2na, \end{align*}

kjer je \( n \in \mathbb{Z} \).

Greenova funkcija je potem

\[ G \left( x, x_0, t, t_0 \right) = \sum\limits_n^{} \left[ G_{\infty} \left( x, x_0 + 2n a, t t_0 \right) - G_{\infty} \left( x, -x_0 + 2na, t, t_0 \right) \right] \]

Sedaj vzamemo posplošeno Greenovo formulo za difuzijo, kjer velja \( f(\vec{r}_0, t_0) = 0 \). Na \( \partial D \) je Greenova funkcija \( G \left( \vec{r}, \vec{r}_0, t, t_0 \right) = 0 \) in iz robnih pogojev sledi, da je \( T \left( \vec{r}_0, t \right) = 0 \).

Preostane nam samo

\[ T \left( x, t \right) = \int\limits_0^a T_0 (x_0) G \left( x, x_0, t, 0 \right) \, \mathrm{d} x_0. \]

Vstavimo v enačbo Greenovo funckijo, ki smo jo izpeljali in dobimo

\begin{align*} T(x, t) &= \frac{1}{\sqrt{4 \pi D t}} \sum\limits_{n = - \infty}^{\infty} \int\limits_0^a T_0 (x_0) \left[ \exp \left\{ - \frac{(x - x_0 - 2na) ^2}{4 D t}\right\} - \exp \left\{ - \frac{(x + x_0 - 2na) ^2}{4 D t} \right\} \right]\, \mathrm{d} x_0 \end{align*}

Rešujemo valovno enačbo za \( c = 1 \)

\[ \nabla ^2 u = \frac{\partial ^2 }{\partial t ^2} u. \]

Definicija Greenove funkcije je še zmeraj ekvivalentna prejšnji

\[ \left( \frac{\partial ^2 }{\partial t ^2} - \nabla ^2 \right) G \left( \vec{r} - \vec{r}_0, t - t_0 \right) = \delta \left( \vec{r} - \vec{r}_0, t - t_0 \right) . \]

Preko Fourierove transformacije dobimo

\[ \left( - \omega ^2 + k ^2 \right) G \left( \vec{k}, \omega \right) = \frac{1}{\sqrt{2 \pi}^{n + 1}}. \]

Obratna Fourierova transformacija pa je

\[ G \left( \vec{r}, t \right) = - \frac{1}{\sqrt{2 \pi}^{n + 1}} \int\limits_{\mathbb{R} ^n}^{} \, \mathrm{d} ^n \vec{k} \int\limits_{\mathbb{R} ^n}^{} \frac{1}{\omega ^2 - k ^2} \exp \left\{ \mathrm{i} \vec{k} \vec{r} - \mathrm{i}\omega t\right\} \, \mathrm{d} \omega. \]

Naš integral ime pole v \( \omega = \pm k \).

Integral bomo ponovno izvrednotili preko izreka o residuih. Zamislimo si zaključeno zanko, ki je sestavljena iz dveh manjših krožnic polmera \( r \to 0 \), ki obkrožita pola na realni osi, premic, ki povezuje polkrožnici, ter večja polkrožnico na negativni imaginarni ravnini z radijem \( R \to \infty \). Hassani diskutira, kako izbira izogibanja pola s krožnico (ali gremo po pozitivni ali negativni polravnini), vpliva na Greenovo funkcijo.

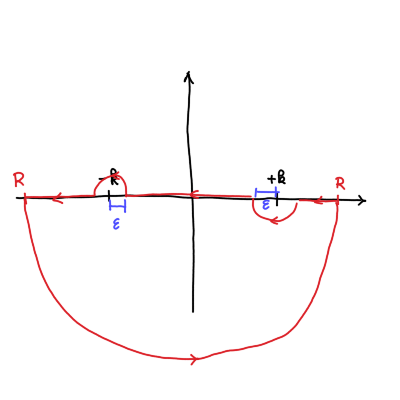
Sami se bomo lotili malo drugačnega postopka. Gremo v prostor \( \vec{r}, \omega \). Definicija Greenove funkcije je potem

\[ \left( - \frac{\omega ^2}{c ^2} - \nabla ^2 \right) G \left( \vec{r}, \omega \right) = \frac{1}{\sqrt{2 \pi}} \delta \left( \vec{r} \right). \]

Po premetavanju elementov dobimo obliko Helmholtzove enačbe

\[ \left( \nabla ^2 + \frac{\omega ^2}{c ^2} \right) G \left( \vec{r}, \omega \right) \cdot \left( - \sqrt{2\pi} \right) = \delta \left( \vec{r} \right) . \]

V treh dimenzijah je rešitev, ki jo poznamo

\[ G \left( \vec{r}, \omega \right) = \frac{1}{4 \pi \sqrt{2 \pi}} \frac{1}{r} \exp \left\{ \pm \mathrm{i} \frac{\omega}{c} r \right\}. \]

Na rešitvi izvedemo obratno Fourierovo transformacijo

\begin{align*} G \left( \vec{r}, t \right) &= \frac{1}{4 \pi 2 \pi r} \int\limits_{}^{} \exp \left\{ \mathrm{i} k r - \mathrm{i} \omega t \right\} \, \mathrm{d} \omega \\ &= \frac{1}{4 \pi 2 \pi r} \int\limits_{}^{} \exp \left\{ \omega \mathrm{i} \left( \pm \frac{r}{c} - t \right) \right\} \, \mathrm{d} \omega \\ &= \frac{1}{4 \pi r} \delta \left( \pm \frac{r}{c} - t \right) \\ &= \frac{1}{4 \pi r} \delta \left( \pm \frac{r}{c} - t \right) \end{align*}

Poudarimo ponovno, da je to rešitev v treh dimenzijah. Rešitvi v eni in dveh dimenzijah sta drastično različni od izračunane.

\[\begin{array}{|c|c|c|} \hline \text{realni } p & k / \omega & \\ \hline \delta \left( \frac{r}{c} - t \right) & \exp \left\{ \mathrm{i} (k x - \omega t )\right\} & \text{retardirana G. f.} \\ \hline \delta \left( - \frac{r}{c} - t \right) & \exp \left\{ \mathrm{i} (- kx - \omega t) \right\} & \text{ avansirana G. f.} \\ \hline \end{array} \]

Avansirana G. f. pravi, da se valovanja širi nazaj v času. Večino časa bomo uporabljali Greenovo funkcijo naprej v času.

Za enačbo

\[ \left( \frac{1}{c ^2} \frac{\partial ^2 }{\partial t ^2} - \nabla ^2 \right) u \left( \vec{r}, t \right) = f \left( \vec{r}, t \right) \]

je posplošena Greenova funkcija

\begin{equation} \label{eq:1} \begin{aligned} u \left( \vec{r}, t \right) = & \int\limits_0^t \, \mathrm{d} t_0 \int\limits_{\mathcal{D}}^{} \, \mathrm{d} ^n \vec{r}_0 G\left( \vec{r}, \vec{r}_0, t, t_0 \right) f \left( \vec{r}_0, t_0 \right) \\ &+ \int\limits_{\mathcal{D}}^{} \left[ \frac{\partial u}{\partial t} \left( \vec{r}_0, 0 \right) G \left( \vec{r}, \vec{r}_0, t, 0 \right) - u \left( \vec{r}_0, 0 \right) \frac{\partial }{\partial t} \left( \vec{r}, \vec{r}_0, t, 0 \right) \right] \\ &+ \int\limits_0^t \, \mathrm{d} t_0 \int\limits_{\partial \mathcal{D}}^{} \mathrm{d}^{n - 1} S_0 \left[ \frac{\partial }{\partial \vec{n}_{0}} u \left( \vec{r}_0, t_0 \right) G \left( \vec{r}, \vec{r}_0, t, t_0 \right) - u \left( \vec{r}_0 , t_0 \right) \frac{\partial }{\partial \vec{n}_{0}} G \left( \vec{r}, \vec{r}, t, t_0 \right) \right] \end{aligned} \end{equation}

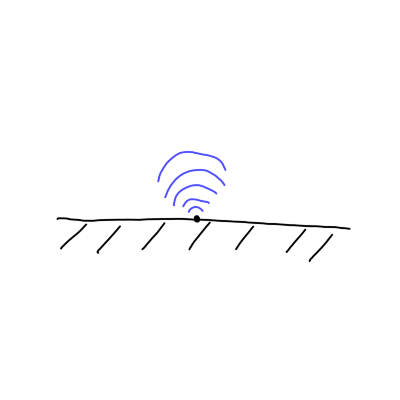
Greenovo funkcijo bomo zapisali kot vsoto dveh Greenovih funkcij na neskončnem območju prek zrcaljenja. Naj bo \( \vec{r} = (x, y, z) \) poljubna točka na polprostoru \( z > 0 \) in naj bo \( \vec{r}^{\, \ast} = (x, y, -z) \) točka \( \vec{r} \) zrcaljena čez premico \( z = 0 \).

Greenovo funkcijo bomo zapisali z retardirano Greenovo funkcijo, saj imamo valovanje, ki se širi naprej v času. Torej

\begin{align*} G \left( \vec{r}, \vec{r}_0, t, t_0 \right) &= G_{ \infty} \left( \vec{r}, \vec{r}_0, t, t_0 \right) - G_{\infty} \left( \vec{r}, \vec{r}_0^{ \, \ast}, t, t_0 \right) \\ &= \frac{1}{4 \pi \left| \vec{r} - \vec{r}_0 \right|} \delta \left( + \frac{\left| \vec{r} - \vec{r}_0 \right|}{c} - \left( t - t_0 \right) \right) - \frac{1}{4 \pi \left| \vec{r} - \vec{r}_0^{ \, \ast} \right|} \delta \left( \frac{\left| \vec{r} - \vec{r}_0^{\, \ast} \right|}{c} - (t - t_0) \right) \end{align*}

V enačbi \ref{eq:1} se zaradi začetnega pogoja \( u (t= 0) = 0 \) izniči drugi integral, zaradi homogenosti enačbe pa prvi integral. V tretjem integralu, ki poteka po meji naše množice, je Greenova funkcija po definiciji enaka \( 0 \).

\[ u \left( \vec{r}, t \right) = \int\limits_0^t \left[ - u \left( \vec{r}_0, t_0 \right) \frac{\partial }{\partial \vec{n}_0} G \left( \vec{r}, \vec{r}_0, t, t_0 \right) \right] \]

Normala zmeraj kaže ven iz območja, torej bo \( \vec{n}_0 = - \hat{e}_z \) in posledično \( \frac{\partial }{\partial \vec{n}_{0}} = - \frac{\partial }{\partial z_0} \). Diferencial površine zapišemo z \( \mathrm{d} S = \mathrm{d} x \mathrm{d} y \).

Zgornji integral se preobrazi v

\begin{align*} u \left( \vec{r}, t \right) &= \int\limits_0^t \iint\limits_{}^{} \left. u \left( \vec{r}_0, t_0 \right) \frac{\partial }{\partial z} G \left( \vec{r}, \vec{r}_0, t, t_0 \right) \right|_{z_0 = 0} \,\mathrm{d S_0} \, \mathrm{d} t_0 \\ &= \iint\limits_{\mathbb{R} ^2}^{} \int\limits_0^t f (t_0) \delta(x_0) \delta(y_0) \left. \frac{\partial }{\partial z_{0}} G \left( \vec{r}, \vec{r}_0, t, t_0 \right) \right|_{z = 0} \,\mathrm{d}t _0 \, \mathrm{d} x_0 \, \mathrm{d} y_0 \\ &= \int\limits_0^t f(t_0) \frac{\partial }{\partial z_{0}} G \left( \vec{r}, z_0 \hat{e}_z, t, t_0 \right) \, \mathrm{d} t_0 \end{align*}

Želimo izračunati odvod Greenove funkcije

\begin{align*} \left. \frac{\partial }{\partial z_{0}} \left[ \frac{1}{\left| \vec{r} \mp z_0 \hat{e}_z \right|} \cdot \delta \left( t - t_0 - \frac{1}{c} \left| \vec{r} \mp z_0 \hat{e}_{z} \right| \right) \right] \right|_{z_0 = 0} &= \left. \left[ - \frac{1}{2} \frac{\pm \left( z \mp z_0 \right) }{\left| \vec{r} \mp z_0 \hat{e}_{z} \right|^3} \cdot \delta \left( t- t_0 - \frac{1}{c} \left| \vec{r} \mp z_0 \hat{e}_z \right| + \frac{1}{\left| \vec{r} \mp z_0 \hat{e}_{z} \right|} \right) \right. \right. \\ & \left. \left. \quad + \frac{1}{\left| \vec{r} \mp z_0 \hat{e}_{z} \right|} \cdot \delta ' \left( t- t_0 - \frac{1}{c} \left| \vec{r} \mp z_0 \hat{e}_{z} \right| + \frac{1}{\left| \vec{r} \mp z_0 \hat{e}_{z} \right|} \right) \cdot \frac{1}{c} \cdot \frac{1 \pm (z \mp z_0)}{\left| \vec{r} \mp z_0 \hat{e}_{z} \right|}\right] \right|_{z_0 = 0} \\ &= \pm \frac{z}{r ^3} \delta \left( t - t_0 - \frac{r}{c} \right) \pm \frac{z}{cr ^2} \delta ' \left( t - t_0 - \frac{r}{c} \right). \end{align*}

Pri zgornji notaciji smo zaradi strnjenega zapisa upoštevali, da velja

\[ \frac{\partial }{\partial z_0} \left| \vec{r} \mp z_0 \hat{e}_z \right| = \frac{1}{2} \frac{\pm \left( z \mp z_0 \right)}{\left| \vec{r} \mp z_0 \hat{e}_z \right|}. \]

To velja za poljubno odvajanje absolutne razlike vektorjev do potence natančno.

Na naslednjem predavanju bomo določili, kaj je odvod funkcije \( \delta \).