Mat3teden13

Naj bo \( n \in \mathbb{N} \), \( a_1, \ldots, a_n \in \mathbb{R} \). Obravnavamo enačbe

\begin{equation} \label{eq:2} \sum\limits_{j=0}^n a_j y^{(j)} = 0 \end{equation}

To je problem primer linearne diferencialne enačbe višjega reda, in sicer

\begin{equation} \label{eq:4} \sum\limits_{j= 0}^n a_j x^j y^{(j)} (x) = b(x), \ b \in \mathbb{R} \end{equation}

Za \( s = -x \) velja

\[ \sum\limits_{j= 0}^n a_j s_j w^{(j)} (s) = \sum\limits_{j=0}^n a^j x^j y^{(j)} (x) \]

če je \( w(s) := y(-x) \). Torej lahko enačbo obravnavamo za \( x > 0 \).

Lokalni ekstrem oz. ekstremala funkcije \( I \) definiramo kot funkcijo \( y\in X \), v kateri ima ekstrem v vsem smereh. To pomeni, da ima za vsako gladko funkcijo \( \eta \), za katero je \( y + \epsilon \eta \in X \) za dovolj majhne \( \epsilon \), na realnih številih (oz. na nekem odprtem intervalu v \( \mathbb{R} \) ) definirana funkcija

\[ \epsilon \mapsto I (y + \epsilon \eta) \]

ekstrem v točki \( 0 \).

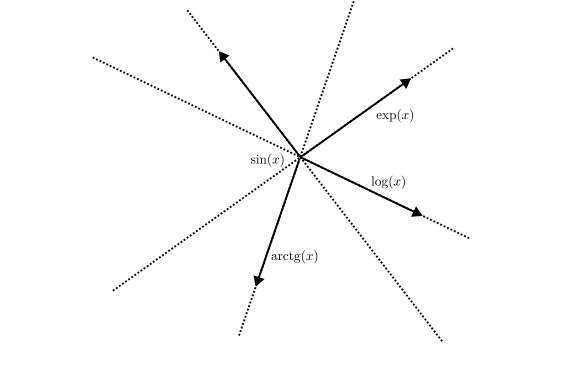
Stacionarna “točka” funkcionala \( I \) je funkcija \( y \in X \), za katero velja, da je

\begin{equation} \label{eq:5} \left. \frac{\mathrm{d} }{\mathrm{d} \epsilon} I (y + \epsilon \eta) \right|_{\epsilon = 0} = 0 \end{equation}

Zožamo npr. na premico \( \mathrm{exp} \) (glej sliko) in tam iščemo ekstrem (kar je pa je potem \( \mathbb{R} \to \mathbb{R} \)) in to naredimo v vseh smereh.

Želimo preprostejši pogoj za \( L, \ y \), ki bo potrebej pogoj za \ref{eq:5}. Temu pogoju pravimo Euler-Lagrangeov pogoj. Naj bo \( J \subset \mathbb{R} \) omejen zaprt interval. Označimo

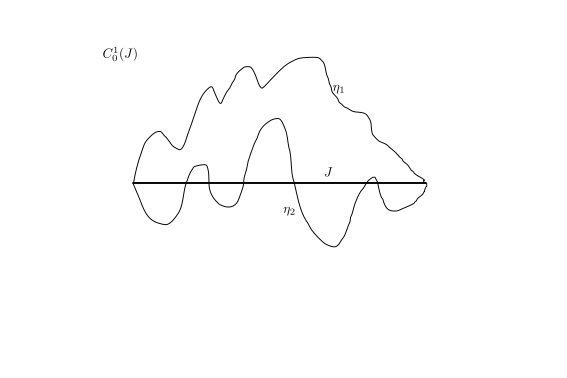
\[ C_0^1 (J) = \left\{ \eta \in C^1(J); \ \left. \eta \right|_{\delta J} = 0 \right\} \]

Množici \( C_0^1 \) pravimo testne funkcije. Ničla v indeksu pove, da ima funkcija v krajišču vrednost 0.

[vstavi skico]

Naj bo \( J = [a, b] \) kot prej in \( f \in C(J) \). Če velja

\begin{equation} \label{eq:7} \int\limits_J^{} f \eta \,\mathrm{d } = 0, \ \forall \eta \in C_0^1 (J) \end{equation}

tedaj je \( f \equiv 0 \) na \( J \) oz. \( \forall x \in J: \ f(x) = 0 \).

Opomba: brez zveznosti ta lema ne drži

Dokaz: Denimo, da sklep ne velja, torej \( f \not \equiv 0 \), torej obstaja \( x\in J \), v katerem \( f(x) \ne 0 \).

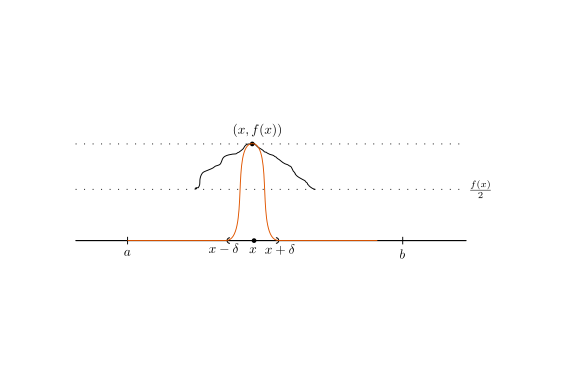
Privzemimo, da je \( f(x) \gneqq 0 \). Ker je \( f \) zvezna, obstaja \( \delta > 0 \) tako, da velja na \( (x - \delta, x + \delta) \cap J \) velja \( f(t) \le \frac{f(x) }{2}; t \in (x - \delta, x + \delta) \cap J \).

Sedaj definiramo

\[ \eta = \begin{cases} \eta \le 0 \\ \eta > 0; \ (x - \delta, x + \delta) \cap J \\ \eta = 0, \text{ else} \end{cases} \]

Sledi

\[ \int\limits_J^{} f \eta\,\mathrm{dx} = \int\limits_{\left( x - \delta, x + \delta \right)\cap J}^{} f \eta \,\mathrm{d x} + \int\limits_{\text{else}}^{} f \eta\,\mathrm{dx} \lneq 0 \]

ker je prvi integral večji od 0, drugi pa je enak 0.

Primer funkcije \( \eta \) je

\[ \eta = \begin{cases} 0, \ x \le 0\\ e^{- \frac{1}{x}}, \ x > 0 \end{cases} \]

Ki jo potem zrcalimo in množimo.

Naj bo \( J = [a, b] \subset \mathbb{R} \) in \( L : J \times \mathbb{R} \times \mathbb{R} \to \mathbb{R} \) zvezno odvedljivana vse spremenljivke. Vzamemo še \( X \subset C^1 (J) \) in naj bo \( y \in X \) takšna, da je

\[ y + C_0^1 (J) \subset X \]

Opomba: če je \( A \) množica in \( f \) funkcija, potem je \( f + A = \left\{ f + g, g \in A \right\} \)

Če je \( y \) stacionarna točka za funkcional \( I: X \to \mathbb{R} \) definiran s predpisom

\[ I(y) + \int\limits_a^b L(x, y, y') \,\mathrm{d x} \]

tedaj \( y \) ustreza Euler-Lagrangeovemu (oznaka za naprej EL) pogoju

\[ L_y (x, y, y') = \frac{\mathrm{d} }{\mathrm{d} x} L_{y'} (x, y, y') \]

Interpretacija: \( L \) je funkcija treh spremenljivk \( u \in J,\ v \in \mathbb{R},\ w \in \mathbb{R} \)

\[ \frac{\partial L}{\partial v} L(x, y(x), y'(x)) = \frac{\mathrm{d} }{\mathrm{d} x} \left[ \frac{\partial L}{\partial w} (x, y(x), y'(x)) \right], \ x \in [a, b] \]

Načeloma sta \( y \) in \( y' \) funkciji \( x \), v tem daljšem zapisu, pa je v resnici odvod po drugi in tretji spremenljivki.

S pomočjo EL se problem iskanja stacionarnih točk funkcionala \( I \) “prevede” na reševanje diferencialne enačbe drugega reda. Ni pa integracije.

Dokaz:

Spomnimo: če je \( y \) stacionarna točka za \( I \) mora po definiciji veljati

\begin{equation} \label{eq:6} \left. \frac{\mathrm{d} }{\mathrm{d} \epsilon} I(y + \epsilon \eta) \right|_{\epsilon=0} = 0, \ \eta \text{ (testno funkcijo)} \end{equation}

Vzamemo torej \( \eta \in C_0^1 (J) \). Po privzetku je \( y + \epsilon \eta \in X \ \forall \epsilon \in \mathbb{R} \). Definiramo funkcijo \( F(I, y, \eta): \mathbb{R} \to \mathbb{R} \) s predpisom:

\[ F(\epsilon) = I (y + \epsilon \eta) \]

Funkcija \( F \) nam je všeč, ker slika iz \( \mathbb{R} \) v \( \mathbb{R} \) in smo na “domačem terenu analize 1”.

\begin{align*} F(\epsilon) &= I(y + \epsilon \eta) \\ &= \int\limits_a^b L(x, y(x) + \epsilon \eta(x), y' + \epsilon \eta'(x) \,\mathrm{d x} \\ \end{align*}

Ker smo privzeli, da je \( y \) stacionarna točka za \( I \), mora veljati \( F'(0) = 0 \) (\ref{eq:6})

Računamo torej

\begin{align*} F'(\epsilon) &= \frac{\mathrm{d} }{\mathrm{d} \epsilon} \int\limits_a^b L(x, y + \epsilon \eta, y' + \epsilon \eta') \,\mathrm{d x} \\ &= \int\limits_a^b \frac{\partial }{\partial \epsilon} L(x, y+\epsilon \eta, y' + \epsilon \eta') \,\mathrm{d x} && \text{ definiramo } \omega_{\epsilon} (x) = (x, y + \epsilon \eta, y' + \epsilon \eta') \\ &= \int\limits_a^b \left[ \frac{\partial L}{\partial u} \left( \omega_{\epsilon} (x) \right) \frac{\partial x}{\partial \epsilon} + \frac{\partial L}{\partial v} \left( \omega_{\epsilon} (x) \right) \frac{\partial \left( y + \epsilon \eta \right)}{\partial \epsilon} + \frac{\partial L}{\partial w} \left( \omega_{\epsilon} (x) \right) \frac{\partial \left( y' + \epsilon \eta' \right)}{\partial \epsilon} \right]\,\mathrm{d x} \\ &= \int\limits_a^b \left[ \frac{\partial L}{\partial v} (\omega_{\epsilon}) \cdot \eta + \frac{\partial L}{\partial w} \left( \omega_{\epsilon} \right) \cdot \eta' \right] \,\mathrm{d x} \end{align*}

Uporabiti moramo pogoj \( F'(0) \).

Definiramo \( \omega_0 = \omega_0 (x) = (x, y(x), y'(x)) \)

\begin{align*} F' (0) &= \int\limits_a^b \left[ \frac{\partial L}{\partial v} \left( \omega_0 \right) \cdot \eta + \frac{\partial L}{\partial w} \left( \omega_0 \right) \cdot \eta' \right]\,\mathrm{d x} \end{align*}

Iz \ref{eq:6} torej dobimo

\begin{equation} \label{eq:8} \int\limits_a^b \left[ \frac{\partial L}{\partial v} \left( \omega_0 \right) \cdot \eta + \frac{\partial L}{\partial w} \left( \omega_0 \right) \cdot \mathbf{\eta'} \right]\,\mathrm{d x}, \ \forall \eta \end{equation}

Če želimo pogoj oblike \ref{eq:7}, moramo integrirati po delih, da se znebimo \( \eta ' \). Iz pogoja \ref{eq:8} z integracijo po delih (tako, da \( \eta' \) integriramo in dobimo \( \eta \)) dobimo

\begin{align*} 0 &= \int\limits_a^b \frac{\partial L}{\partial v} (\omega_0) \eta \,\mathrm{d x} + \left. \eta \cdot \frac{\partial L}{\partial w} \right|_{x = a}^{x=b} - \int\limits_a^b \eta \frac{\mathrm{d} }{\mathrm{d}x} \left[ \frac{\partial L}{\partial w} (\omega_0) \right] \,\mathrm{d x} \\ &= \int\limits_a^b \left( \frac{\partial L}{\partial v} (\omega_0) - \frac{\mathrm{d} }{\mathrm{d} x} \left[ \frac{\partial L}{\partial w} (\omega_0) \right] \right) \eta\,\mathrm{d x} + \frac{\partial L}{\partial w} (\omega_0) \eta(b) - \frac{\partial L}{\partial w} (\omega_0)\eta(a) && \text{ predpostavka je } \eta \in C_0^1 (J) \land \eta(a) = \eta(b) = 0 \\ &= \int\limits_a^b \left( \frac{\partial L}{\partial v} (\omega_0) - \frac{\mathrm{d} }{\mathrm{d} x} \left[ \frac{\partial L}{\partial w} (\omega_0) \right] \right)\eta\,\mathrm{d x} \end{align*}

Dokazali smo, če je \( y \) stacionarna točka za \( I \), tedaj je

\[ \int\limits_a^b \left( \frac{\partial L}{\partial v} (\omega_0) - \frac{\mathrm{d} }{\mathrm{d} x} \left[ \frac{\partial L}{\partial w} (\omega_0) \right] \right)\eta \,\mathrm{d x} = 0, \ \forall \eta \in C_0^1 (J) \]

Uporabimo variacijsko lemo \ref{eq:7} in dobimo

\[ \frac{\partial L}{\partial v} (\omega_0) - \frac{\mathrm{d} }{\mathrm{d} x} \left[ \frac{\partial L}{\partial w} (\omega_0) \right] = 0 \]

to pa je ravno (EL). QED.

Spomnimo se: s fiksnimi krajišči mislimo

\[ X \subset \left\{ f \in C^1 (J), \ f(a) = \alpha, f(b) = \beta \right\} \]

za neka vnaprej podana, predpisana \( \alpha, \beta \).

Gibljiva krajišča za \( f \in X \), kjer \( f \) na robu \( J \) ni predpisan. Če imamo gibljiva krajišča, razmišljamo tako: še vedno dobimo

\begin{equation} \label{eq:9} \int\limits_a^b \left( \frac{\partial L}{\partial v} (\omega_0) - \frac{\mathrm{d} }{\mathrm{d} x} \left[ \frac{\partial L}{\partial w} (\omega_0) \right] \right)\eta \,\mathrm{d x} + \eta(x) \left. \frac{\partial L}{\partial w} (\omega_0(x)) \right|_{x=a}^{x=b} = 0, \ \forall \eta \in C^1(J) \end{equation}

Ni nujno, da je \( C_0^1(J) \)! Če pogoja, da so fiksna krajišča, ni več, ni potrebe več po tem, da bi predpisovali, kakšne vrednosti imajo različne funkcije \( \eta \) v krajiščih.

V posebnem velja \ref{eq:9} velja tudi za \( \eta \in C_0^1 (J) \). Vemo, da to implicira (EL) pogoj, torej se \ref{eq:9} prevede na

\[ \left. \eta(x) \cdot \frac{\partial L}{\partial w} \left( \omega_0 (x) \right) \right|_{x=a}^{x=b} = 0, \ \forall \eta \in C^1 (J) \]

Če določimo določimo krajišča, se zgornja formula samo prevede na prejšnji problem s fiksnimi krajišči.

Če imamo produkt \( \eta(a) \cdot C = 0, \forall \eta \in C^1 (J) \implies C = 0 \). Iz tega sledi transverzalni pogoj

\begin{equation} \label{eq:10} \frac{\partial L}{\partial w} (\omega_0 (a)) = \frac{\partial L}{\partial w} (\omega_o (b)) = 0 \end{equation}

To je v bistvu samo nadomestek za \( y(a) = \alpha, \ y(b) = \beta \), ko imamo gibljiva krajišča.